문 17. 다음 글의 내용이 참일 때, 갑이 반드시 수강해야 할 과목은?
갑은 A~E 과목에 대해 수강신청을 준비하고 있다. 갑이 수강하기 위해 충족해야 하는 조건은 다음과 같다.
○ A를 수강하면 B를 수강하지 않고, B를 수강하지 않으면 C를 수강하지 않는다.
○ D를 수강하지 않으면 C를 수강하고, A를 수강하지 않으면 E를 수강하지 않는다.
○ E를 수강하지 않으면 C를 수강하지 않는다.
① A ② B ③ C ④ D ⑤ E
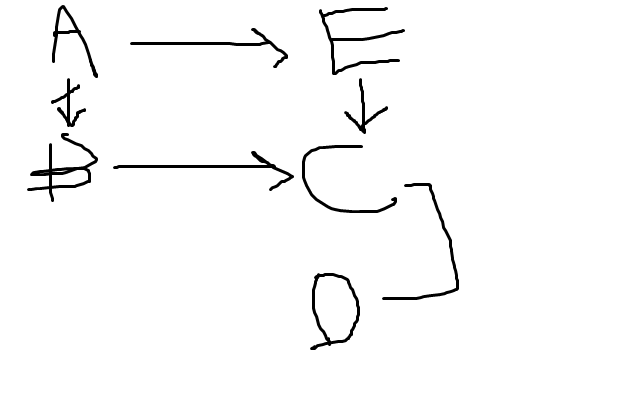
대충 이케이케 그려서 D다.
C의 선수과목(prerequisite)이 B, E인데
E의 선수과목이 A이므로 C를 들으려면
결국 A, B 다 들어야 한다. 그런데
처음에 A를 들으면 B 못 듣는다 했으므로 ABCE계열 사이에 모순이 있다.
결국 D를 들을 수밖에 없다.
통상적인 졸업사정/수강신청 조건 설명은 저런 식으로 하지 않을 텐데 하는 의문은 든다.
A를 수강했으면 B를 수강할 수 없다.
C를 수강하기 위해 D를 선수과목으로 이미 들었어야만 한다. (D를 수강하지 않았으면 C를 수강하지 못한다)
이런 식이 애매하지 않은 명확한 표현일 것이다.
물론 문제에서는 한 학기에 동시에 수강신청 하는 시나리오를 제시했으므로 정확히 선수과목이라 하기도 조금 애매하긴 하다.
이런 시나리오도 가능하다. 학생이 나름의 원칙을 정해서 수강신청 하는 것이다.
예를 들어 컴퓨터 학과에서 운영체제 계열과 응용프로그램 계열 2가지를 모두 들어야 하는데 학과에서는 학생의 선택 대로 1학기 또는 2학기 중 원하는 학기에 아무 과목이나 들을 수 있게 하지만, 이 학생은 어떤 한 계열 수강 신청에 실패했을 경우 해당 계열의 다른 과목도 신청하지 않는 식으로(즉 한 학기에 한 계열만 선택) 나름의 원칙을 정할 수도 있는 것이다.
문제에는 'X면 Y이다'라는 관계는 한 번도 등장하지 않는다.
선수과목 관계는 'X가 아니면 Y가 아니다'이다.
그럼 'A면 B가 아니다' 이건 뭔가? 예를 들어 이런 것이다. 선형대수학 들었으면 선형대수학개론 수강 금지. 수학과 이산수학 들었으면 컴퓨터학과 이산수학 수강 금지.
D를 수강하지 않으면 C를 수강하고...이건 뭔가? 앞의 예에서 계열 선택이다(운영체제 또는 응용프로그램) 그럼 반대로, C를 수강하지 않으면 D를 수강해야 하는가(mutually exclusive)? 의문이 들지만 그냥 넘어간다(그게 답이니까 언급을 안 한 것인지도?ㅋ)
좀 현실적인 예를 위 문제에 끼워맞춰 볼까...
A=선형대수학을 수강하면 B=선형대수학개론을 수강하지 않는다. (말이 됨. )
B=선대개론을 수강하지 않으면 C=컴퓨터그래픽을 수강하지 않는다. (말이 됨)
D=운영체제를 수강하지 않으면 C=컴퓨터그래픽을 수강한다. (말이 됨)
A=선형대수를 수강하지 않으면 E=이산수학을 수강하지 않는다. (말이 안 됨)
E=이산수학을 수강하지 않으면 C=그래픽을 수강하지 않는다. (말이 안 됨)
결국 이산수학이 잘못이다 이렇게 된 이상 이번 학기는 D=운영체제로 간다(뭐라고!?)
농담이고
그냥 기계적으로 푸는 법도 있다.










이런 더러운 계산을 안 틀리고 할 수 있으면 된다.
(합집합=덧셈, 교집합=곱셈)
민간에는 그다지 알려져 있지 않은 것인데,
If A then B 라는 표현은 사실
(not A) or B
와 같다.
그래서 위와 같은 집합 계산으로 환원된다.
이 문제의 선지는 쉬운 내용을 일부러 헷갈리게 섞어놓은 것이다
1) 선수과목(if not A then not B)
2) 쉬운 과목 재수강 금지(if A then not B)
3) 계열 선택(if not A then B)
3가지 유형을 한 문장 안에 섞어 놓거나, 다른 항에 옮겨놓았다.