Wolframalpha plot 연습 중입니다 :)
고등학교 수준까지만 써야지.
10년도 더 전에 본 거라 가물가물하당.
제품 P와 Q의 재료는 모두 S1, S2만 쓰이는데 배합 비율이 다르다.
P 하나 만드는 데 S1이 5개, S2가 2개 필요하다.
Q 하나 만드는 데 S1이 5개, S2가 4개 필요하다.
근데 운송 문제로 S1은 하루에 25 단위, S2는 하루에 16 단위 밖에 못 쓴다고 한다.
한편 이 동네는 너무 작아서 하루에 아무리 많이 팔아 봤자 P는 5개 팔린다고 한다.
P의 가격은 1만원, Q의 가격은 5만원이다.
하루 수익을 최대로 하려면 P랑 Q를 몇 개씩 만드는 게 좋을까?
-----------
일단 최대값, 최소값을 떠올리고 부등식(등식이 아님)을 떠올리는 게 좋다.
\(p=P의\ 개수,\ q=Q의\ 개수\)라 하고 문제의 조건을 다시 쓰면 아래와 같다:
일단 최대값, 최소값을 떠올리고 부등식(등식이 아님)을 떠올리는 게 좋다.
\(p=P의\ 개수,\ q=Q의\ 개수\)라 하고 문제의 조건을 다시 쓰면 아래와 같다:
\[0 \le p \le 5\]
\[0 \le q \]
$$5p+5q\le25 \Leftrightarrow p+q\le5$$
\[2p+4q \le 16 \Leftrightarrow p+2q \le 8 \]
일 때
\(수익\ i=p+5q\)를 최대화 하라.
\(수익\ i=p+5q\)를 최대화 하라.
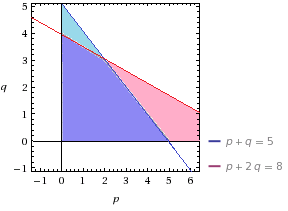
빗금친 부분이 부등식이 성립하는 부분이다.
직선 \(i=p+5q\)를 이리저리 움직여 보면, 그냥 Q만 만드는 \((p=0, q=4)\) 게 제일 좋음을 알 수 있다.
그림을 그려볼 때는 기울기가 중요하다. \(i=p+5q\)의 기울기가 -1/5이기 때문에 (0, 5)가 답이 된 것이다. 기울기가 -1과 -1/2 사이였다면 (2, 3)이 답이었겠지...
변수 개수가 늘면 행렬도 써야하고 풀기 어려워진다고 한다. Simplex method라나...
그냥 컴터로 해! Monte Carlo처럼 점 다 대입해도 되겠구만 ㅋ
직선 \(i=p+5q\)를 이리저리 움직여 보면, 그냥 Q만 만드는 \((p=0, q=4)\) 게 제일 좋음을 알 수 있다.
변수 개수가 늘면 행렬도 써야하고 풀기 어려워진다고 한다. Simplex method라나...
그냥 컴터로 해! Monte Carlo처럼 점 다 대입해도 되겠구만 ㅋ
No comments:
Post a Comment